高斯函数,基于高斯函数的图像处理技术解析与应用

你知道吗？在数学的世界里，有一个超级神奇的函数，它就像是一个万能的魔术师，能够把复杂的问题变得简单易懂。这个神奇的函数，就是——高斯函数！今天，就让我带你一起探索这个数学界的宝藏吧！

什么是高斯函数？

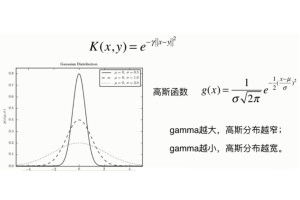
高斯函数，又称为正态分布函数，它描述的是一种在自然界和人类社会广泛存在的概率分布。想象你手中有一把五颜六色的糖果，当你随机挑选糖果时，你可能会发现某些颜色的糖果比其他颜色的糖果多。这种颜色的分布，其实就是正态分布，而高斯函数就是描述这种分布的数学工具。

高斯函数的起源

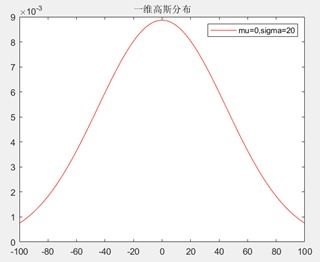
高斯函数最早是由德国数学家卡尔·弗里德里希·高斯在19世纪初提出的。当时，高斯正在研究天体运动，他发现天体运动的轨迹往往呈现出一种特定的分布规律。为了描述这种规律，高斯提出了正态分布的概念，并给出了相应的数学公式。

高斯函数的数学表达式

高斯函数的数学表达式如下：

\\[ f(x) = \\frac{1}{\\sqrt{2\\pi\\sigma^2}} e^{-\\frac{(x-\\mu)^2}{2\\sigma^2}} \\]

其中，\\( f(x) \\) 表示高斯函数的概率密度函数，\\( \\mu \\) 表示均值，\\( \\sigma \\) 表示标准差。这个公式看起来有点复杂，但其实它就像是一个神奇的魔法咒语，能够把各种复杂的数据转化为简单的概率分布。

高斯函数的应用

高斯函数的应用范围非常广泛，几乎涵盖了自然科学、社会科学和工程技术等各个领域。以下是一些高斯函数的典型应用：

1. 统计学：在统计学中，高斯函数被用来描述数据的分布规律，帮助我们更好地理解数据的特征。

2. 物理学：在物理学中，高斯函数被用来描述粒子的运动轨迹、电磁场的分布等。

3. 生物学：在生物学中，高斯函数被用来描述生物体的生长、繁殖等过程。

4. 金融学：在金融学中，高斯函数被用来描述股票价格、汇率等金融变量的分布规律。

5. 图像处理：在图像处理中，高斯函数被用来进行图像平滑、去噪等操作。

高斯函数的局限性

虽然高斯函数在各个领域都有广泛的应用，但它也有一些局限性。首先，高斯函数只能描述正态分布的数据，对于其他类型的数据，高斯函数可能并不适用。其次，高斯函数的数学表达式较为复杂，对于一些非专业人士来说，理解起来可能会有一定的难度。

高斯函数，这个数学界的宝藏，就像一位神奇的魔术师，能够把复杂的问题变得简单易懂。它不仅丰富了数学的宝库，还为各个领域的研究提供了有力的工具。让我们一起探索这个神奇的函数，感受数学的魅力吧！